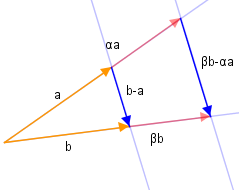
Strahlensatz

ss.png
Zu zeigen ∣αa∣∣a∣=∣βb∣∣b∣  ⟺  (b−a)∣∣(βb−αa)\dfrac {|\alpha a|} {|a|} =\dfrac{|\beta b|}{|b|}\iff (b-a)||(\beta b-\alpha a) also α=β  ⟺  (b−a)∣∣(βb−αa)\alpha=\beta\iff (b-a)||(\beta b-\alpha a)
(b−a)∣∣(βb−αa)(b-a)||(\beta b-\alpha a)   ⟺  ⟨b−a,(βb−αa)i⁡⟩=0\iff \langle b-a,(\beta b-\alpha a)\i\rangle=0   ⟺  α⟨a,ai⁡⟩+β⟨b,bi⁡⟩−α⟨b,ai⁡⟩−β⟨a,bi⁡⟩=0\iff\alpha \langle a,a\i\rangle+\beta\langle b,b\i\rangle-\alpha\langle b,a\i\rangle-\beta\langle a,b\i\rangle=0   ⟺  α⟨a,bi⁡⟩−β⟨a,bi⁡⟩=0\iff \alpha\langle a,b\i\rangle-\beta\langle a,b\i\rangle=0   ⟺  α=β\iff\alpha=\beta (weil aa und bb beliebige Vektoren)
Es gilt auch: βb−αaαa=b−aa  ⟺  α=β\dfrac{\beta b-\alpha a}{\alpha a} =\dfrac {b-a} a \iff \alpha=\beta
 
 

Die Furcht vor der Mathematik steht der Angst erheblich näher als der Ehrfurcht.

Felix Auerbach

Copyright- und Lizenzinformationen: Diese Seite ist urheberrechtlich geschützt und darf ohne Genehmigung des Autors nicht weiterverwendet werden.
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld  • Dοrfplatz 25  •  17237 Blankеnsее  • Tel.: 01734332309 (Vodafone/D2)  •  Email: cο@maτhepedιa.dе
Datenschutzerklärung

 

Ebene Geometrie mit komplexen Zahlen