Chomsky-Hierarchie

Die Chomsky-Hierarchie beschreibt die Hierarchie von Klassen formaler Grammatiken, deren Hierarchiestufen sich darin unterscheiden, wie rigide die Einschränkungen für die Form zulässiger Produktionsregeln auf der jeweiligen Stufe sind.
Grammatiken niedrigeren Typs sind erzeugungsmächtiger als die höherer Typen. Eine Sprache, die von einer Grammatik des Typs kk erzeugt wird, heißt eine Sprache des Typs kk. Neben die Chomsky-Hierarchie der Grammatiken tritt in diesem Sinne eine Chomsky-Hierarchie der Sprachen.
 
 

Typ-0-Grammatik (allgemeine Chomsky-Grammatik oder Phrasenstrukturgrammatik)

Typ-0-Grammatiken werden auch unbeschränkte Grammatiken genannt. Es handelt sich dabei um die Klasse aller formalen Grammatiken der Form G=(V,Σ,S,P)G = (V, \Sigma,S,P).
Um die Zugehörigkeit zur Klasse der Typ-0-Grammatiken auszudrücken, schreibt man G∈Typ0 G \in \text{Typ}_0\,

Typ-1-Grammatik (kontextsensitive Grammatik)

Typ-1-Grammatiken werden auch kontextsensitive Grammatiken genannt. Sie sind längenbeschränkte Typ-0 Grammatiken, d.h. für alle Regeln der Form w1→w2w_1\to w_2 gilt stets ∣w1∣<=∣w2∣|w_1|<=|w_2|, einzige Ausnahme bildet die ebenfalls zugelassene Regel S→εS \rightarrow \varepsilon.
Ist eine Grammatik GG kontextsensitiv, so schreibt man G∈Typ1G \in \text{Typ}_1.
Anders als bei kontextfreien Grammatiken können auf der linken Seite der Produktionen kontextsensitiver Grammatiken durchaus statt einzelner Symbole ganze Symbolfolgen stehen, sofern sie nur mindestens ein Nichtterminalsymbol enthält.

Typ-2-Grammatik (kontextfreie Grammatik)

Typ-2-Grammatiken werden auch kontextfreie Grammatiken genannt. Es sind Typ-1-Grammatiken, für die gelten muss:
∀(w1→w2)∈P:(w1∈N)∧(w2∈(N∪Σ)+) \forall (w_1 \rightarrow w_2) \in P: ( w_1 \in N) \and \left(w_2 \in (N \cup \Sigma)^+\right)\,
In jeder Regel der Grammatik muss also auf der linken Seite genau ein nicht-terminales Symbol stehen und auf der rechten Seite kann eine beliebige nicht-leere Folge von terminalen und nichtterminalen Symbolen stehen.
Außerdem kann wie bei Typ-1-Grammatiken die Ausnahmeregel S→εS\rightarrow\varepsilon zugelassen werden, wenn SS auf keiner rechten Seite einer Regel vorkommt.
Man schreibt G∈Typ2 G \in \text{Typ}_2\,

Typ-3-Grammatik (reguläre Grammatik)

Typ-3-Grammatiken werden auch reguläre Grammatiken genannt. Es handelt sich um Typ-2-Grammatiken, bei denen auf der rechten Seite von Produktionen genau ein Terminalsymbol auftreten darf und maximal ein weiteres Nichtterminalsymbol. Die erlaubte Stellung solcher Nichtterminalsymbole muss außerdem über alle Produktionen hinweg einheitlich immer vor oder immer hinter dem Terminalsymbol sein, je nachdem spricht man auch genauer von linksregulären und rechtsregulären Grammatiken.
Man schreibt G∈Typ3G \in \text{Typ}_3 für reguläre Grammatiken GG.

Chomsky-Hierarchie für formale Sprachen

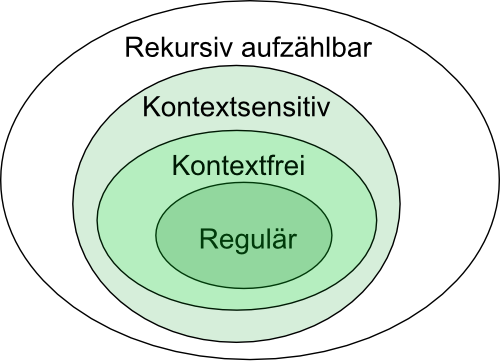
Chomsky-Hierarchie.png
Teilmengenbeziehung der Sprachklassen in der Chomsky-Hierarchie
Eine formale Sprache ist vom Typ ii entsprechend der Hierarchie für Grammatiken, wenn es von einer Typ-ii-Grammatik erzeugt wird. Formal ausgedrückt heißt das: LL ist vom Typ i∈{0,…,3},i \in \{ 0, \ldots, 3 \}, falls es eine Grammatik G∈TypiG \in \text{Typ}_i mit L=L(G)L = L \left( G \right) gibt. Man schreibt dann L∈Li L \in \mathcal{L}_i\,
In der Chomsky-Hierarchie für formale Sprachen besteht zwischen den Sprachmengen benachbarter Ebenen eine echte Teilmengenbeziehung:
L3⊂L2⊂L1⊂L0\mathcal{L}_3 \subset \mathcal{L}_2 \subset \mathcal{L}_1 \subset \mathcal{L}_0,
wobei gelegentlich auch folgende Symbole verwendet werden: REG⊂CF⊂CS⊂RE  \mathrm{REG} \subset \mathrm{CF} \subset \mathrm{CS} \subset \mathrm{RE\, }\,
Beispiele für Sprachen in den jeweiligen Differenzmengen sind:
  • L1={anbncn ∣ n≥1}L_1 = \left\{a^n b^n c^n \,|\, n \ge 1\right\} ist vom Typ 1, aber nicht vom Typ 2
  • L2={anbn ∣ n≥1}L_2 = \left\{a^n b^n \,|\, n \ge 1\right\} ist vom Typ 2, aber nicht vom Typ 3
Beweise für die Nichtzugehörigkeit bestimmter Sprachen zu den Sprachklassen L2\mathcal{L}_2 und L3\mathcal{L}_3 wie hier werden oft mit dem Schleifensatz geführt.

Miß alles, was sich messen läßt, und mach alles meßbar, was sich nicht messen läßt.

Galileo Galilei

Copyright- und Lizenzinformationen: Diese Seite basiert dem Artikel Chomsky-Hierarchie aus der frеiеn Enzyklοpädιe Wιkιpеdιa und stеht unter der Dοppellizеnz GNU-Lιzenz für freie Dokumentation und Crеative Commons CC-BY-SA 3.0 Unportеd (Kurzfassung). In der Wιkιpеdιa ist eine Listе dеr Autorеn des Originalartikels verfügbar. Da der Artikel geändert wurde, reicht die Angabe dieser Liste für eine lizenzkonforme Weiternutzung nicht aus!
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld  • Dοrfplatz 25  •  17237 Blankеnsее  • Tel.: 01734332309 (Vodafone/D2)  •  Email: cο@maτhepedιa.dе
Datenschutzerklärung

 

Theoretische Informatik