Grundbegriffe der ebenen Geometrie
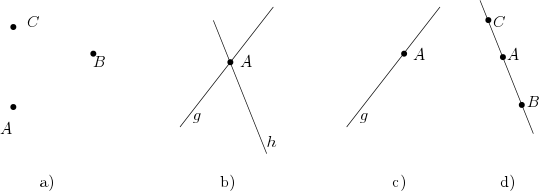
Lageverhältnisse von Geraden und Punkten
Die grundlegenden Objekte der ebenen Geometrie sind Punkte und Geraden.
Jeweils zwei verschiedene Punkte bestimmen eindeutig eine Gerade und zwei verschiedene Geraden haben höchstens einen Punkt gemeinsam. Haben zwei Geraden keinen Punkt gemeinsam so sind sie parallel ( und in der nebenstehenden Grafik). Man schreibt dafür .
Punkte werden mit großen Buchstaben wie , , ... und Geraden mit kleinen Buchstaben wie , , usw. bezeichnet.
In der nebenstehenden Grafik liegen die Punkte , und auf der Geraden und die Punkte und auf der Geraden . Die Geraden und schneiden sich also im Punkt . Die Gerade ist parallel zur Geraden .
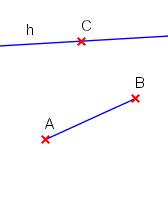
Liegen zwei Punkte und auf einer Geraden, so heißt der Abschnitt zwischen und Strecke, mit der Bezeichnung .
Liegt ein Punkt auf einer Geraden, so teilt er diese in zwei Halbgeraden. Alle Punkte einer Halbgeraden bilden einen Strahl, ausgehend vom Punkt .
Religion und Mathematik sind nur verschiedene Ausdrucksformen derselben göttlichen Exaktheit.
Kardinal Michael Faulhaber
Copyright- und Lizenzinformationen: Diese Seite ist urheberrechtlich geschützt und darf
ohne Genehmigung des Autors nicht weiterverwendet werden.
Anbieterkеnnzeichnung: Mathеpеdιa von Тhοmas Stеιnfеld
• Dοrfplatz 25 • 17237 Blankеnsее
• Tel.: 01734332309 (Vodafone/D2) •
Email: cο@maτhepedιa.dе